Eaman Jahani | Unequal Diffusion in Networks

In this project, we propose a random network model that illustrates how brokerage in network structure can lead to unequal diffusion. Furthermore, we present empirical results that confirm the role of brokerage in constraining information diffusion in real-world networks. Network brokerage occurs when a few nodes in the network have higher propensity to connect with an out-group than other in-group nodes. While brokers play an integral role in connecting otherwise disconnected communities across structural holes [1], they can nevertheless act as a bottleneck when compared to a similar network with cross-group ties uniformly distributed across the network. Because brokers hold a disproportionate number of cross-group ties, they can constrain diffusion of information from one group to another.

To completely account for unequal diffusion in a network, one needs to not only look at homophily or assortativity on paths of length 1, but also on the extent of assortativity of all possible diffusion paths of varying length. Here, we show brokerage can increase assortativity along diffusion paths of length 2 in ways that simple measures of homophily fail to capture. Any variation in cross-group linking among nodes of a group leads to higher unequal diffusion than expected by models that explicitly fit assortativity [2]. As the first step, we show this phenomena analytically by building a latent space network model [3] with a parameter that controls the degree of heterogeneity in cross-group linking. Figure 1 shows what happens as we modify this parameter: while assortativity along paths of length 1 decreases as cross-type edges appear, assortativity along paths of length 2, akin to diffusion assortativity, can remain high if the network exhibits high brokerage.

Figure 1. Assortativity along paths of length 1 and 2 vary as the distribution of nodes on the latent space varies. Each point corresponds to a network model as we vary the latent space distribution. Different colors correspond to varying levels of brokerage. For a fixed level of assortativity on paths of length 1, as brokerage increases, assortativity on paths of length 2 also increases.

As the second step, we investigate the extent of this phenomena in real-world networks. We find that most networks exhibit higher susceptibility to unequal diffusion than expected by simple measures of homophily across various grouping variables (e.g. gender or race). Finally, we develop a variant of the Stochastic Block Model [4] that parametrizes the cross-group degree of each node, and by doing so fits not only assortativity on paths of length 1, but also assortativity on paths of length 2 and 3. This model significantly improves the fit over SBM on empirical networks and accurately predicts the susceptibility of a network to unequal diffusion. For example, Figure 2 shows how the observed assortativity along paths of length 2 compares against the regular degree-corrected SBM model versus our model which accounts for brokers.

Figure 2. Top row shows the observed assortativity on paths of length 2 versus its distribution from the MLE of the degree-corrected Stochastic Block Model (DC-SBM). The assortativity is measured along gender in two middle school networks. Bottom row illustrates the same comparison in our model which accounts for cross-group degree variation or brokerage. In total, 30% of our school networks have higher assortativities than expected by DC-SBM, whereas none of the networks have this inconsistency under our model.

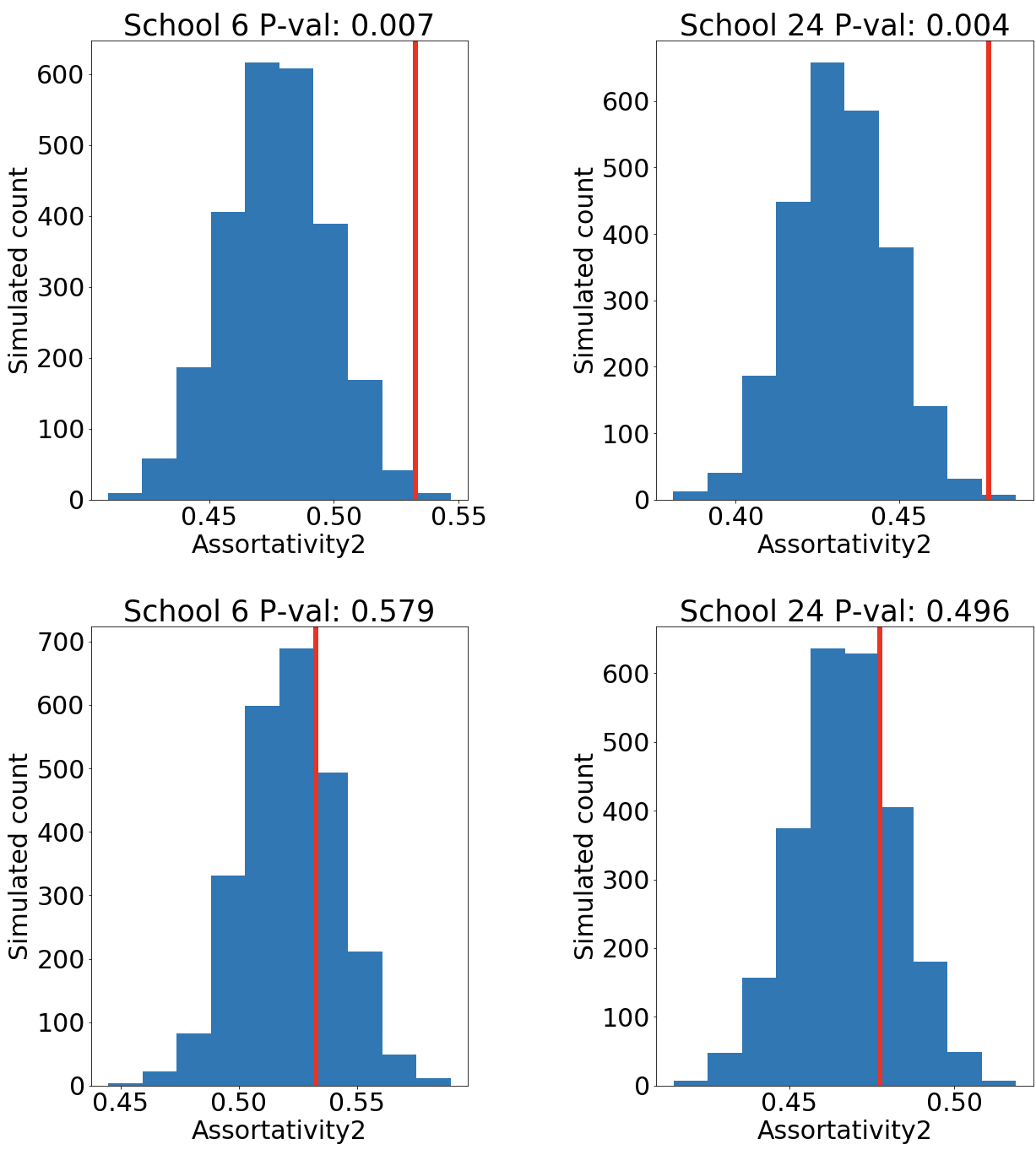
Our modeling results show that networks that have similar levels of assortativity or homophily could have very different degrees of susceptibility to unequal diffusion. This variation arises from the extent to which the connections between different social classes are controlled by a small group of individuals acting as brokers. Our findings provide an important policy implication: while brokers act as a bridge between communities, they nevertheless control the flow of information. Networks that heavily depend on brokers for connectivity suffer from unequal diffusion of information much greater than networks whose cross-group links are equally distributed. This happens because the existence of brokers not only hampers diffusion to the first degree but also to the second degree, the whole group ends up with less pathways to information sources.

References

[1] Ronald S Burt. Structural holes: The social structure of competition. Harvard university press, 2009.
[2] Mark EJ Newman. Mixing patterns in networks. Physical Review E, 67(2):026126, 2003.
[3] Peter D Hoff, Adrian E Raftery, and Mark S Handcock. Latent space approaches to social network analysis. Journal of the American Statistical Association, 97(460):1090–1098, 2002.
[4] Brian Karrer and Mark EJ Newman. Stochastic blockmodels and community structure in networks. Physical review E, 83(1):016107, 2011.